Chuyển hình thức thi viết sang thi trắc nghiệm, đó là lý do mà các bạn cần quan tâm nhiều hơn các công thức tính nhanh. Bài viết dưới đây sẽ hướng dẫn các bạn cụ thể các công thức tính nhanh thể tích khối chóp với các dạng và bài tập thật chi tiết.
Xem thêm:
- [Toán học] Công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện
- Tổng hợp các công thức tính thể tích tứ diện trong Oxyz chi tiết
- Công thức tính thể tích khối chóp đều và bài tập có lời giải
Khối chóp là gì?
Trong hình học, khối chóp(hay là hình chóp) là một khối đa diện, được hình thành bằng các kết nối của một diểm với một đa giác. Điểm đó được gọi là đỉnh, các mặt bên là một tam giác khi kết hợp giữa đỉnh và cạnh đáy. Đa giác có thể là một tam giác, tứ giác, ngũ giác, lục giác,…
Công thức chung tính thể tích khối chóp
Thể tích khối chóp (hình chóp)
Công thức chung khi tính thể tích khối chóp là:
V =1/3(h.S)
Trong đó:
- V là thể tích hình chóp
- h là chiều cao hình chóp tính từ đỉnh
- S là diện tích đa giác đáy

Cách tính các diện tích đa giác thường gặp
Để có thể tính được thể tích khối chóp thì tính diện tích đáy rất quan trọng. Dưới đây là các dạng tính diện tích các hình đa giác bạn cần nhớ.
- Hình vuông: S = a2
- Hình chữ nhật: S = a.b
- Hình thoi: S = a2.Sin(gocgiua) = (duongcheo.duongcheo)/2
- Hình thang: S = [(dlớn +dnhỏ).h]/2
- Tam giác đều: S = a2.√3/4
- Tam giác vuông: S = (a.b)/2
- Tam giác thường: S = (b.c.SinA)/2 = (a.h)/2 = a.b.c/4R = p.r = √p(p-a)(p-b)(p-c)
Công thức tính nhanh thể tích khối chóp qua các dạng chính
Dạng 1: Cho sẵn đường cao – chóp có cạnh bên vuông góc đáy
V=(h.S)/3
Với dạng bài này thì đã có thể xác định được h, bạn chỉ cần tính diện tích mặt đáy (S) theo công thức phía trên.
Dạng 2: Chóp có mặt bên vuông góc với đáy
V=(h.S)/3
Với dạng bài này thì bạn cần xác định chiều cao khối trụ (h). Và h chính là đường cao của tam giác vuông góc với mặt phẳng. Từ đó ta sẽ có nhiều cách để có thể tính ra h.
Dạng 3: Chóp đều hoặc chóp có cạnh bên bằng nhau
V=(h.S)/3
Chóp tam giác đều (đáy là tam giác đều) & Chóp tứ giác đều (đáy là hình vuông) vì vậy chân đường cao sẽ trùng với tâm đường tròn ngoại tiếp đáy.
Bài tập và đáp án
Bài tập 1: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, góc giữa cạnh bên và mặt đáy bằng 600 .Tính thể tích khối chóp.
A. V = (√3.a3)/12
B. V = (√3.a3)/4
C. V = (4√3.a3)/9
D. V = (9√3.a3)/4
Lời giải:
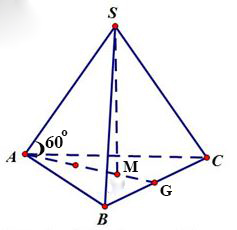
Có ∆ABC đều cạnh 3a ⇒ Sđáy =(3a)2.√3/4 = (9.a2√3)/4 (1)
Lấy (SA,ABC) = 60o
Ta có: AG = 2/3.AM = 2/3.3a.√3/2 = a√3 ⇒ ∆SAG,G^=90o
⇒ tan60o=SG/AG SG = AG.tan60o = √3.a√3 = 3a (2)
Từ (1) và (2) ⇒ Vchóp = 1/3.3a.9a3.√3/4 = (9√3.a3)/4
Đáp án: D
Bài tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều; mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S. SA = a√3, SB = a. TÍnh thể tích khối chóp S.ABC?
A. V = a3/3
B. V = a3/4
C. V = a3/2
D. V = a3/6
Lời giải:
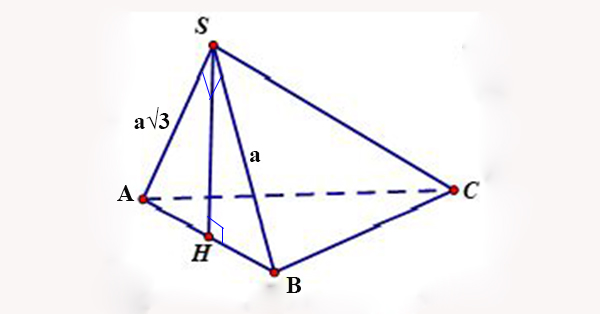
Ta có: (SAB)⊥(ABC) tại AB
⇒SH ⊥ AB ⇒ SH ⊥ (ABC)
+) ∆SAB, S^=90o AB = √(SA2 + SB2)
⇒SH = (SA.SB)/AB = (a√3.a)/2a = a√3/2 (1)
+) Sđáy=(2a)2.√3/4=a2√3 (2)
Từ (1) và (2) ⇒ V = 1/3.a2.√3.a√3/2 = a3∕2
Đáp án: C
Bài tập 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA⊥(ABCD). Cạnh bên SB hợp với đáy một góc 600. Tính thể tích khối chóp S.ABCD.
A. V = (a3√3)/4
B. V = a3√3
C. V = (a3√3)/3
D. V = (a3√3)/6
Lời giải:
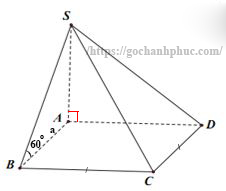
Ta có:
+) SA⊥(ABCD) ⇒ SA = h
+) (SB,ABCD)=60o ⇔
+) Xét ∆SBA, Tan60o= SA/AB ⇒ SA = tan60o.AB
⇒ SA = a√3
Đáy là hình vuông, suy ra: Shv = a2 ➞ V= 1/3.a√3.a2 = (a3.√3)/3
Đáp án : C
Bài viết đã trình bày cụ thể những công thức tính nhanh thể tích khối chóp và có những bài tập có đáp án. Qua bài viết hy vọng các bạn có thể thêm những kiến thức bổ ích. Nếu có câu hỏi gì hãy bình luận bên dưới nhé.








