Công thức tính độ dài đường trung tuyến và bài tập có lời giải

Đường trung tuyến là kiến thức khá quan trọng trong môn toán. Hôm nay Top Nổi Bật sẽ giúp các em ôn tập lý thuyết, công thức tính độ dài đường trung tuyến và bài tập để các em hiểu rõ hơn nhé.

>>Xem thêm

• Công thức tính đường cao trong tam giác vuông, cân, đều, thường và bài tập có lời giải
• Công thức tính diện tích hình tam giác vuông, cân, đều, thường theo cấp
• Công thức tính cạnh huyền tam giác vuông và bài tập có lời giải
• Công thức tính tọa độ trung điểm và bài tập minh họa dễ hiểu

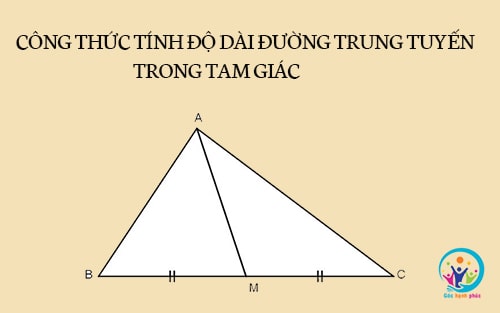
Đường trung tuyến là gì?

Đường trung tuyến của 1 đoạn thẳng là 1 đường thẳng đi qua trung điểm của đường thẳng đó

Đường trung tuyến trong tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới các cạnh đối diện nó. Mỗi tam giác có 3 đường trung tuyến

Tính chất của đường trung tuyến

Trong tam giác thường, vuông, cân đều có tính chất của đường trung tuyến khác nhau.

Đường trung tuyến trong tam giác thường gồm 3 tính chất như sau:

• 3 đường trung tuyến trong tam giác cùng đi qua 1 điểm, điểm đó cách đỉnh tam giác một khoảng bằng độ dài của đường trung tuyến đi qua đỉnh đó.
• Giao điểm của 3 đường trung tuyến được gọi là trọng tâm
• Vị trí trọng tâm trong tam giác: Trọng tâm của 1 tam giác cách mỗi đỉnh 1 khoảng bằng độ dài đường trung tuyến đi qua đỉnh đó.

Tính chất đường trung tuyến của tam giác vuông:

• Đường trung tuyến trong tam giác vuông ứng với cạnh huyền bằng nửa cạnh huyền
• Trong tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông

Tính chất đường trung tuyến của tam giác đều, tam giác cân

• Đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đấy, và chia tam giác thành 2 tam giác bằng nhau

Công thức tính độ dài đường trung tuyến

Công thức tính độ dài đường trung tuyến của cạnh bất kỳ bằng căn bậc 2 của một phần hai tổng bình phương hai cạnh kề trừ một phần tư bình phương cạnh đối.

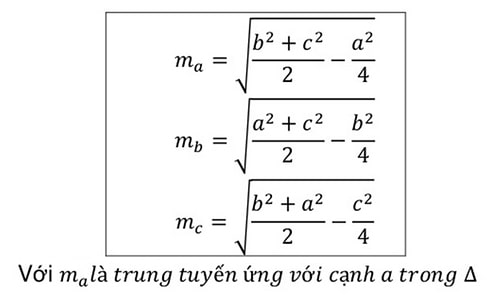
Trong đó: a, b ,c lần lượt là các cạnh trong tam giác

                 m_a, m_b, m_{c lần} lượt là những đường trung tuyến trong tam giác

Bài tập có lời giải về cách tính độ dài đường trung tuyến

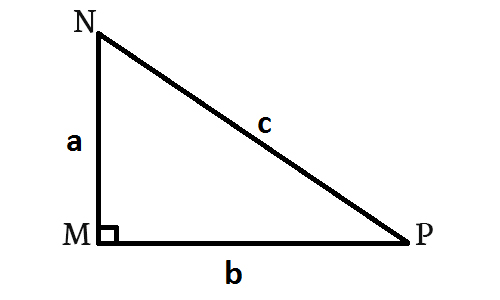
Bài tập 1: Cho tam giác MNP biết NP = 20cm, PM = 16cm, MN = 14cm. Tính độ dài các đường trung tuyến của tam giác MNP

Lời giải

a = NP = 20cm, b = PM = 16cm, c = MN = 14cm

Gọi độ dài đường trung tuyến từ những đỉnh M, N, P của ∆MNP lần lượt là m_a, m_b, m_c

Áp dụng công thức tính đường trung tuyến trong tam giác ta có:

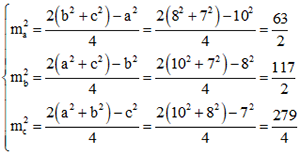
Vì độ dài các đường trung tuyến là độ dài đoạn thẳng do đó:

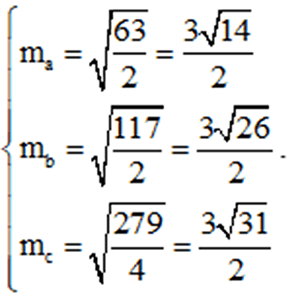
Bài tập 2: Cho tam giác MNP cân tại M, biết MN = MP = 8cm, NP = 7cm. Kẻ đường tuyến MI. Chứng minh MI ﬩ NP

Lời giải

Ta có MI là đường trung tuyến của ∆MNP nên IN = IP

Mặt khác ∆MNP là tam giác cân tại M

=> MI vừa là đường trung tuyến vừa là đường cao

=> MI ﬩ NP

Trên đây là toàn bộ kiến thức về đường trung tuyến trong tam giác để các bạn học sinh, bậc phụ huynh, và các thầy cô giáo cùng tham khảo. Những kiến thức về môn toán sẽ được góc hạnh phúc cập nhật liên tục. Do vậy, nếu như có bài tập gì khó, hoặc có phần nào không hiểu hãy để lại bình luận bên dưới chúng tôi sẽ giải đáp thắc mắc của bạn trong thời gian sớm nhất.