Công thức tính bán kính đường tròn ngoại tiếp đang là kiến thức khá quan trọng nhưng có rất nhiều em chưa biết về nó. Hôm nay chúng tôi sẽ liệt kê những công thức, cách tính bán kính đường tròn nội tiếp và cho một số bài tập có lời giải để các em hiểu và nhớ công thức lâu hơn.
>>Xem thêm
- Các công thức tính đường kính hình tròn và bài tập có lời giải
- Các công thức tính bán kính hình tròn và bài tập có lời giải chi tiết
- Đường tròn có bao nhiêu trục đối xứng
- Công thức tính bán kính đường tròn nội tiếp tam giác
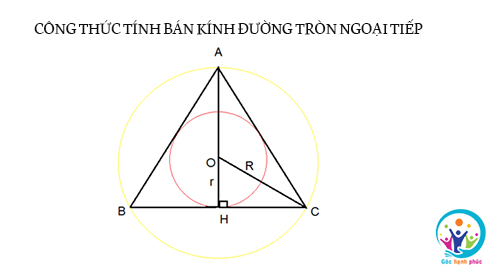
Đường tròn ngoại tiếp là gì?
Đường tròn ngoại tiếp tam giác hay còn được gọi là tam giác nội tiếp đường tròn là đường tròn đi qua 3 đỉnh của tam giác
Tính chất đường tròn ngoại tiếp:
- Mỗi tam giác chỉ có 1 đường tròn ngoại tiếp
- Tâm của đường tròn ngoại tiếp tam giác là giao điểm giữa 3 đường trung trục của tam giác
- Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền
- Đối với tam giác đều, tâm đường tròn ngoại tiếp và nội tiếp tam giác trùng với nhau
Các công thức tính bán kính đường tròn ngoại tiếp
Công thức tính bán kính đường tròn ngoại tiếp tam giác bằng tích của 3 cạnh tam giác chia bốn lần diện tích:
R = (a x b x c) : 4S
Công thức tính bán kính đường tròn ngoại tiếp của góc A
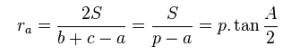
Công thức tính bán kính đường tròn ngoại tiếp của góc B
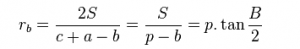
Công thức tính bán kính đường tròn ngoại tiếp của góc C
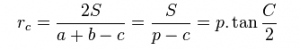
4 cách tính bán kính đường tròn ngoại tiếp
Cách 1: Dựa vào định lý sin trong tam giác
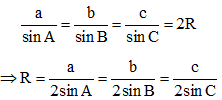
Cách 2: Dựa vào diện tích trong tam giác
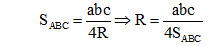
Cách 3: Dựa vào hệ tọa độ
R = OA = OB = OC
Cách 4: Sử dụng tam giác vuông
Tâm của đường tròn ngoại tiếp trong tam giác vuông là trung điểm của cạnh huyền. Do vậy, bán kính đường tròn ngoại tiếp tam giác vuông là bằng nửa độ dài của cạnh huyền đó.
Bài tập có lời giải về bán kính đường tròn ngoại tiếp
Bài tập 1: Cho tam giác MNP vuông tại N, và MN = 6cm, NP = 8cm. Xác định bán kính đường tròn ngoại tiếp tam giác MNP bằng bao nhiêu?
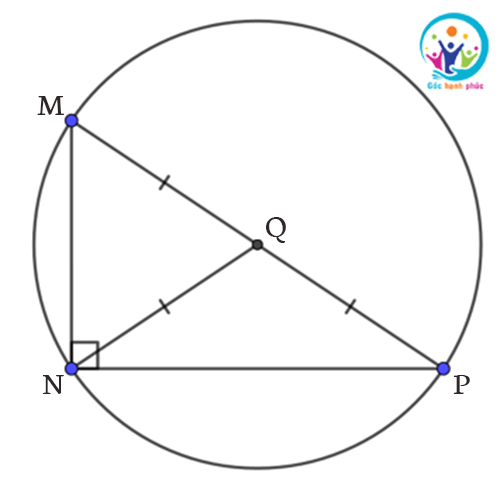
Lời giải
Áp dụng định lý pytago ta có:
PQ = 1/2 MP
=> NQ = QM = QP = 5cm
Gọi D là trung điểm MP
=> ∆MNP vuông tại N có NQ là đường trung tuyến ứng với cạnh huyền MP
=> Q là tâm đường tròn ngoại tiếp ∆MNP
=> Đường tròn ngoại tiếp ∆MNP là trung điểm Q của cạnh huyền và bán kính đường tròn ngoại tiếp MNP là R = MQ = 5cm
Đáp số: 5cm
Bài tập 2: Cho tam giác MNP đều với cạnh bằng 12cm. Xác định tâm và bán kính đường tròn ngoại tiếp ∆MNP?
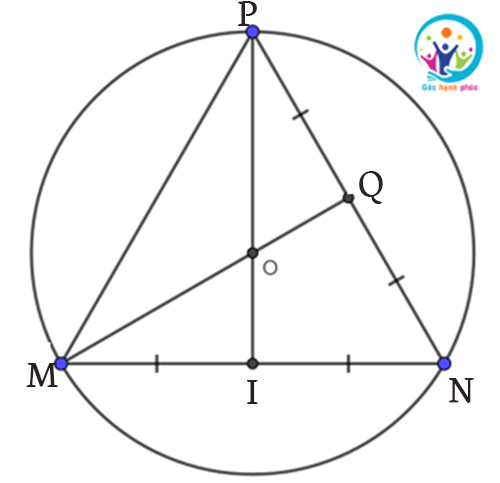
Lời giải
GỌi Q, I lần lượt là trung điểm của cạnh NP, MN và MQ giao với PI tại O
Vì ∆MNP đều nên đường trung tuyến cũng là đường cao, đường phân giác, đường trung trực của tam giác
=> O là tâm của đường tròn ngoại tiếp
=> ∆MNP có PI là đường trung tuyến nên PI cũng là đường cao
Từ đó áp dụng định lý pytago
PI2 = MP2 – MP2
= 122 – 62
= 108cm
=> PI = 6√3cm
Bởi O là trọng tâm của ∆MNP nên:
PO = 2/3PI
= 2/3 x 6√3
= 4√3cm
=> Tâm của đường tròn ngoại tiếp ∆MNP là trọng tâm O và bán kính là PO = 4√3cm
Như vậy, để tính bán kính đường tròn ngoại tiếp tam giác thì có rất nhiều cách giải khác nhau. Tùy vào từng chủ đề bài tập mà các em học sinh hãy áp dụng đúng công thức nhé. Nếu như có khó khăn trong việc giải bài toán hãy để lại bình luận bên dưới, chúng tôi sẽ đồng hành giải những khó khăn đó.







