[Toán học] Công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện

Mặt cầu ngoại tiếp khối đa diện là gì? Công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện? Và các bài tập có lời giải giúp bạn hiểu cặn kẽ hơn về mặt cầu ngoại tiếp khối đa diện.

Xem thêm:

• [Giải đáp] Feet là gì? Chuyển đổi 1 feet bằng bao nhiêu m?
• Công thức tính vận tốc trung bình trên quãng đường gồm 2 đoạn s1 và s2 là gì?
• Tổng hợp các công thức tính thể tích tứ diện trong Oxyz chi tiết

Mặt cầu ngoại tiếp khối đa diện là gì?

Mặt cầu ngoại tiếp khối đa diện là hình cầu đi qua mọi đỉnh của khối đa diện.

Lý thuyết cơ bản của mặt cầu ngoại tiếp khối đa diện:

• Bán kính mặt cầu ngoại tiếp : R
• Diện tích mặt cầu ngoại tiếp: S=4.π.R²
• Thể tích mặt cầu ngoại tiếp: V = (4.π.R³)/3

Các dạng mặt cầu ngoại tiếp khối đa diện:

• Mặt cầu ngoại tiếp khối đa diện có cạnh bên vuông góc với đáy
• Mặt cầu ngoại tiếp khối đa diện hình chóp đều
• Mặt cầu đa diện có mặt bên vuông góc với đáy

Công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện

Mặt cầu ngoại tiếp quan trọng là chúng ta cần xác định được bán kính(R).

Với mỗi dạng mặt cầu ngoại tiếp khối đa diện sẽ có cách tính bán kính riêng. Sau đây là cách tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện.

Dạng 1: Khối đa diện có cạnh bên vuông góc đáy.

Công thức:

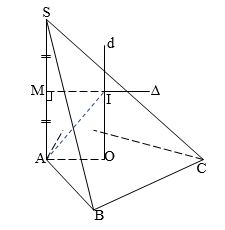
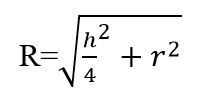
Trong đó:

• R là bán kính khối cầu ngoại tiếp
• h là chiều cao
• r là bán kính đường tròn ngoại tiếp đáy

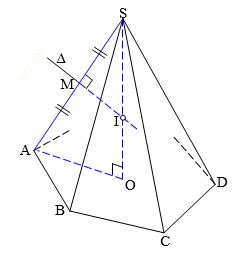
Dạng 2: Khối đa diện chóp đều hoặc các cạnh bên bằng nhau

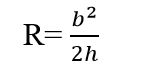
Trong đó:

• R là bán kính khối cầu ngoại tiếp
• h là chiều cao
• b là độ dài cạnh bên

Dạng 3: Mặt cầu đa diện có mặt bên vuông góc với đáy

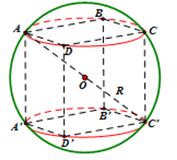
• Hình hộp chữ nhật:

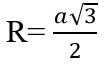
Trong đó:

• a là cạnh huyền vuông góc với đáy
• R là bán kính đường tròn ngoại tiếp

Bài tập có lời giải về mặt cầu ngoại tiếp khối đa diện

Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tại A, SA vương góc với mặt phẳng (ABCD) và SC=4a. Tính bán kính mặt cầu ngoại tiếp hình chóp.

Đáp án:

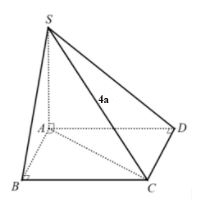
Ta có : BC⊥AB và BC⊥SA ⇒ BC⊥(SAB) ⇒ BC⊥SB

Tương tự ta cũng chứng minh được: CD ⊥ SD

Ta có: SA ⊥ (ABCD) ⇒ SA ⊥ AC

Ba điểm A, B, D cùng nhìn SC dưới một góc vuông.

Như vậy, bán kính mặt cầu S.ABCD là R=SC/2=4a/2=2a

Bài 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E và F lần lượt là trung điểm của BC và CD. Tính bán kính R của khối cầu ngoại tiếp hình chóp S.CEF. Chọn đáp án đúng.

A. R= (a√29)/8

B. R=(5a√3)/12

C. R=(a√37)/6

D. R=(a√93)/12

Lời giải:

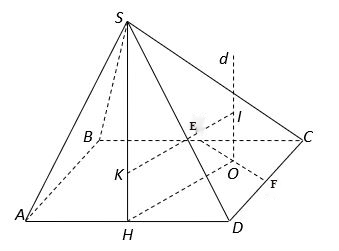
Gọi H là trung điểm của AD ➝ SH ⊥ (ABCD)

Ta thấy tâm I nằm trên trục d đi qua trung điêm O của EF và ⊥(ABCD), I, S cùng phía với mặt phẳng ABCD.

Ta có:

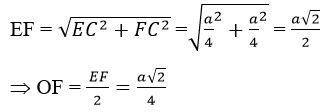
∆HFO vuông tại N ta có:

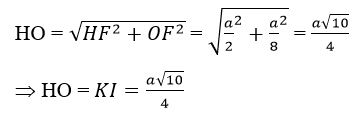
Ta có: OC² + OI² = R² = IK² + KS²

Đặt OI = x ta có:

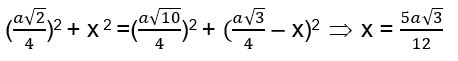
Như vậy ta có:

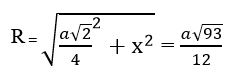
Đáp án: D

Trên đây là nội dung về mặt cầu ngoại tiếp và công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện. Hy vọng những kiến thức Góc Hạnh Phúc mang lại giúp bạn hiểu rõ hơn về mặt cầu ngoại tiếp.