Công thức tính chu vi hình tam giác là kiến thức toán học cơ bản được phổ cập từ chương trình toán học lớp 2, lớp 3 và được sử dụng thường xuyên về sau. Hình tam giác có 4 loại cơ bản: tam giác thường, tam giác vuông, tam giác cân và tam giác đều. Vì vậy bài viết sẽ cung cấp chi tiết cách tính chu vi tam giác và ví dụ cụ thể cho từng loại tam giác để các bạn dễ học, dễ thực hành nhất.
Xem thêm:
1. Cách tính chu vi tam giác có 3 cạnh a b c
Chu vi hình tam giác bằng tam giác cơ bản bằng tổng chiều dài 3 cạnh của tam giác P = a + b + c (I). Công thức có thể áp dụng cho tất cả các loại tam giác khác nhau.
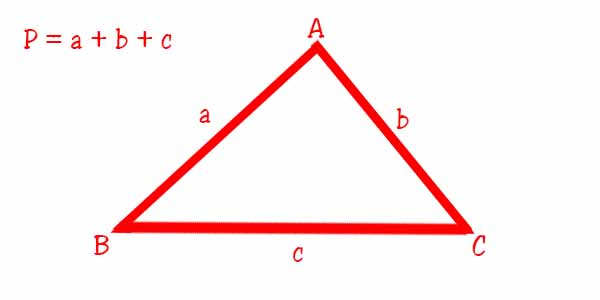
Trong đó:
- P là chu vi tam giác cần tính
- a, b, c là độ dài 3 cạnh của hình tam giác đó.
Ví dụ: Tính chu vi hình tam giác có độ dài 3 cạnh là 5 cm, 9 cm và 12 cm?
Lời giải: Dựa vào công thức tính chu vi tam giác (I) ta có đáp án là: P = 5 + 9 + 12 = 35 (cm)
2. Cách tính chu vi tam giác vuông
Tam giác vuông là tam giác có 1 góc vuông 90 độ, gọi 2 cạnh góc vuông là a và b, cạnh huyền là c.
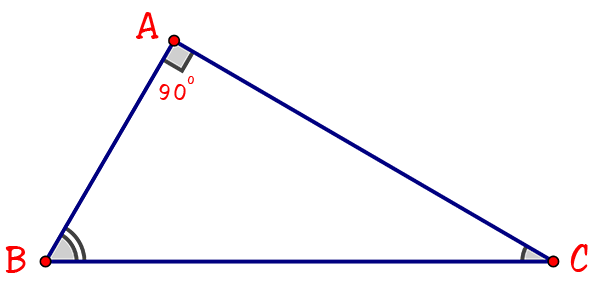
Công thức tính chu vi tam giác vuông là:
P = a + b + c (II)
Trong đó:
- P là chu vi tam giác
- a, b là 2 cạnh góc vuông, c là cạnh huyền.
Ví dụ 1: Tính chu vi tam giác vuông ABC với độ dài AB = 3cm, AC = 4cm, BC = 5cm?
Lời giải: Dựa theo công thức tính chu vi tam giác (II) ta có đáp án là: P = 3 + 4 +5 = 12 (cm).
Lưu ý: Đây là lời giản khi tính chu vi tam giác lớp 2 khi biết độ dài 3 cạnh
Ví dụ 2: Tính chu vi tam giác vuông ABC với độ dài AB = 5, AC = 7?
Lời giải: Muốn tính chu vi tam giác ta cần đi tìm độ dài cạnh còn lại là BC. Áp dụng định lý Pytago trong tam giác vuông ta có cạnh huyền:
BC ² = AB ² + AC ²
BC ² = 6 ² + 8 ² = 36 + 64 = 100
BC = √100 = 10
Vậy chu vi tam giác: P = 6 + 8 + 10 = 24 (cm)
Lưu ý: Đây là bài toán áp dụng định lý Pytago lớp 7 trong tam giác vuông
3. Công thức tính chu vi tam giác cân
Tam giác cân là tam giác có 2 cạnh bằng nhau và 2 góc kề bằng nhau. Đỉnh của tam giác cân là giao điểm của 2 cạnh bên bằng nhau.
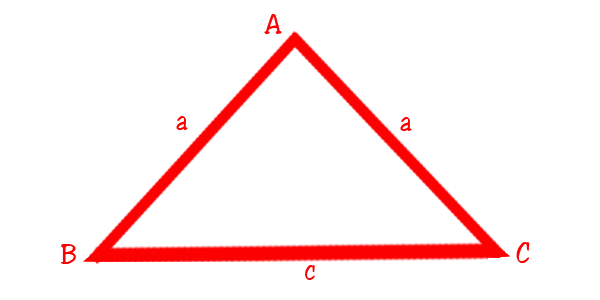
Công thức tính chu vi tam giác là:
P = a + a + c = 2 x a + c
Trong đó:
- P là chu vi tam giác cân
- a là độ dài 2 cạnh bên
- c là độ dài cạnh đáy
Ví dụ: Cho tam giác cân tại A với chiều dài AB = 5cm, BC = 8cm. Tính chu vi tam giác cân ABC?
Lời giải: Áp dụng công thức tính chu vi tam giác cân ta có đáp án: P = 5 + 5 + 8 = 18 cm.
4. Công thức tính chu vi tam giác đều
Tam giác đều là tam giác có 3 cạnh bằng nhau và 3 góc bằng nhau là 60 độ.
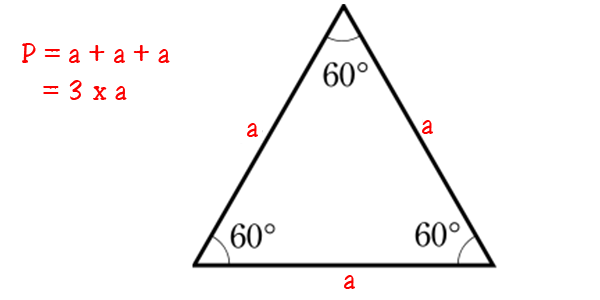
Công thức tính tam giác đều là:
P = a + a + a hoặc P = 3 x a
Trong đó:
- P là chu vi tam giác đều
- a là chiều dài cạnh của tam giác
Ví dụ: Tính chu vi tam giác đều có độ dài cạnh là 6 cm.
Lời giải: Dựa theo công thức tính chu vi tam giác đều ta có đáp án:
P = 6 + 6 + 6 = 18 cm
Lưu ý: Tam giác đều là tam giác đặc biệt ngoài 3 cạnh bằng nhau thì các góc trong cũng có số đo độ bằng nhau là 60 độ.
Tính chu vi tam giác để làm gì?
- Nắm bắt được công thức toán học trong chương trình học.
- Là nền tảng cơ bản cần nắm vững để làm các bài toán liên quan như tính diện tích hình tam giác, tính đường cao,… ở các lớp tiếp theo.
- Vận dụng vào thực tiễn để tính toàn các vật thể hình tam giác.
Bài viết trên đây mong rằng cung cấp cho em, các bạn và quý phụ huynh có thêm tư liệu để học tập, giảng dạy và nắm vững kiến thức lớp 2, lớp 3 trong bài tính chu vi tam giác.







