Công thức đường chéo hình bình hành đang là mối quan tâm của những em học sinh lớp 5, rất nhiều em học sinh đã không nhớ công thức và nhầm lẫn khi làm bài tập. Mà công thức này khá quan trọng, được vận dụng và áp dụng vào nhiều bài tập giải toán hình học của các lớp. Do vậy, bài viết hôm nay chúng tôi sẽ chia sẻ lý thuyết, dấu hiệu nhận biết, công thức, cách tính và bài tập kèm lời giải về đường chéo hình bình hành.
>>Xem thêm:
- Công thức tính chiều cao hình bình hành và bài tập có lời giải
- Công thức tính diện tích hình tứ giác và bài tập có lời giải

Đường chéo hình bình hành là gì?
Đường chéo hình bình hành là các đường không dài bằng nhau và không vuông góc, nhưng nó cắt nhau tại trung điểm.
Dấu hiệu nhận biết đường chéo hình bình hành
- Khi hai đường chéo cắt nhau tại tâm điểm
- Độ dài các đường chéo hình bình hành không bằng nhau và cũng không vuông góc
- Trong hình bình hành có 2 đường chéo bằng nhau chính là hình chữ nhật
- Trong hình bình hành có 2 đường chéo vuông góc với nhau chính là hình thoi
Công thức tính đường chéo hình bình hành chuẩn nhất
Công thức tính đường chéo hình bình hành bằng căn bậc 2 của bình phương độ dài các cạnh trừ 2 nhân độ dài các cạnh nhân cos các góc được tạo bởi hai cạnh kề nhau.
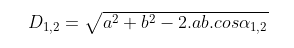
Trong đó: D1,2 là đường chéo hình bình hành
a, b là các cạnh của hình bình hành
α1, α2 là các góc được tạo bởi 2 cạnh kề nhau của hình bình hành
α1 + α2 = 180ο
Bài tập kèm lời giải về cách tính đường chéo hình bình hành
Bài tập 1: Cho hình bình hành ABCD, Gọi J, K theo thứ tự là trung điểm của cạnh CD và AB. Biết đường chéo BD cắt AJ, UK theo thứ tự là MN. Chứng minh rằng DM = MN = NB
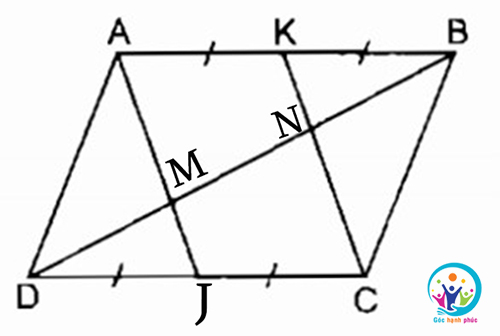
Lời giải:
Ta có: AB = CD (Theo tính chất hình bình hành)
AK = ½ AB
CJ = ½ CD
AK = CJ (1)
Mặt khác: AB // CD
AK // CJ (2)
Từ (1) Và (2) ta được tứ giác AKCJ là hình bình hành bởi có 1 cặp cạnh đối song song và bằng nhau.
AJ // CK
Trong ∆ABM ta có:
K là trung điểm của cạnh AB
AJ // CK hay KN // AM nên ta được BN = MN (theo tính chất đường trung bình của hình tam giác)
Trong đó ∆DCN ta có:
J là trung điểm của cạnh DC
AJ // CK hay JM // CN nên DM = MN (Theo tính chất đường trung bình của hình tam giác
DM = MN = NB
Bài tập 2: Cho hình bình hành MNPQ biết MN = 12cm, NP = 14cm, PQ = 16cm. Hỏi MP.
Lời giải:
Gọi K là giao điểm của đường chéo MP và NP
MK là đường trung tuyến của tam giác MNQ
Áp dụng theo công thức tính đường trung tuyến ta được
MK2 = (MN2 + MQ2) : 2 – (NQ2 : 4)
Vì K là trung điểm của cạnh MP nên MP = 2 x MK
Đáp án các bạn thay số vào công thức theo gợi ý ở trên nhé.
Bài tập 3: Cho hình bình hành MNPQ biết chu vi hình bình hành bằng 20dm, chu vi tam giác MNQ bằng 18dm. Tính độ dài cạnh NQ.
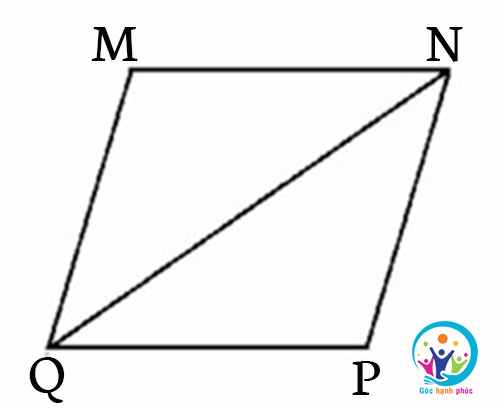
Lời giải
Chu vi hình bình hành bằng MNPQ = 10dm => (MN + PQ) x 2 = 20dm
MN + MQ = 20 : 2 = 10dm
Chu vi của ∆MNQ = MN + MQ + NQ = 18dm
NQ = 18 – (MN +MQ)
= 18 – 10
= 8dm
Đáp án: Độ dài cạnh NQ bằng 8dm
Như vậy, với công thức tính đường chéo hình bình hành ở trên sẽ giúp các em học sinh nhớ công thức lâu hơn và áp dụng để làm bài tập tốt nhất. Ngoài ra, các bậc cha mẹ cũng nên tham khảo tài liệu về công thức hình bình hành của chúng tôi để có thể hướng dẫn và dạy con làm bài tập tại nhà hiệu quả nhất nhé. Nếu như có bài tập nào khó, hoặc còn điều gì đang băn khoăn hãy để lại bình luận bên dưới chúng tôi sẽ giúp giải đáp mọi thắc mắc nhanh nhất.








