Khi bắt đầu bước vào lớp 1, lớp 2 ở tiểu học các em đã bắt đầu học về tam giác. Tuy nhiên đó chỉ là những kiến thức, công thức và bài tập đơn giản, và khi lên lớp 4, lớp 5 các em bắt đầu đi sâu vào những công thức và bài tập khó hơn như công thức tính đường cao trong tam giác. Bài viết hôm nay chúng tôi sẽ giới thiệu các kiến thức về đường cao của hình tam giác vuông, cân, đều, thường và các dạng bài tập liên quan có lời giải.
>>Xem thêm:
- Công thức tính diện tích hình tam giác vuông, cân, đều, thường theo cấp
- Cách tính chu vi hình tam giác vuông, cân, đều, thường trong toán học
Định nghĩa đường cao hình tam giác là gì?
Đường cao hình tam giác hay còn gọi là chiều cao của hình tam giác là 1 đoạn thẳng nối từ một đỉnh và vuông góc với cạnh đối diện. Cạnh đối diện đó còn được gọi là đáy ứng với chiều cao. Độ dài chiều cao hình tam giác là khoảng cách giữa đỉnh và đáy.
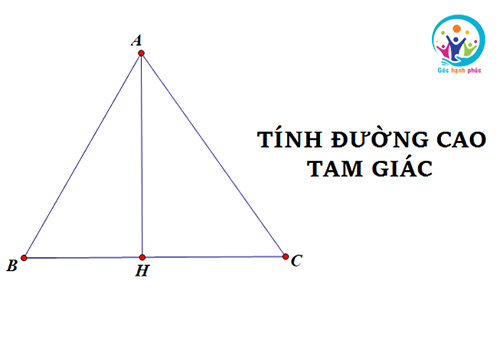
Tính chất của đường cao hình tam giác
- Trong tam giác cân, đường trung trực của cạnh đáy cũng là đường trung tuyến, đường phân giác, đường cao xuất phát từ đỉnh đối diện của cạnh đó
- Trực tâm của tam giác nhọn trùng với trục tâm của đường tròn nội tiếp tam giác được tạo bởi 3 đỉnh là chân 3 đường cao từ 3 đỉnh đến các cạnh tương ứng
- 3 đường cao của tam giác cùng đi qua 1 điểm
Công thức tính đường cao trong tam giác vuông, cân, đều, thường
Có rất nhiều cách, công thức tính chiều cao trong tam giác, khi biết độ dài 3 cạnh thì dùng công thức heron như sau:
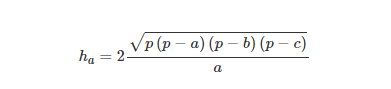
Trong đó: ha là đường cao tam giác
a, b, c lần lượt là các cạnh trong tam giác
p là nửa chu vi hình tam giác
Công thức tính nửa chu vi hình tam giác:
P = (a + b + c) : 2
Công thức tính đường cao trong tam giác vuông
Ví dụ minh họa: Giả sử cho tam giác vuông ABC vuông tại A
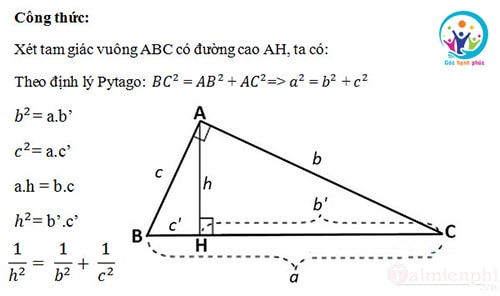
Trong đó: a, b , c lần lượt là những cạnh của tam giác vuông
Công thức tính đường cao trong tam giác cân
Ví dụ minh họa: Giả sử cho tam giác ABC cân tại A. và đường cao AH vuông tại H
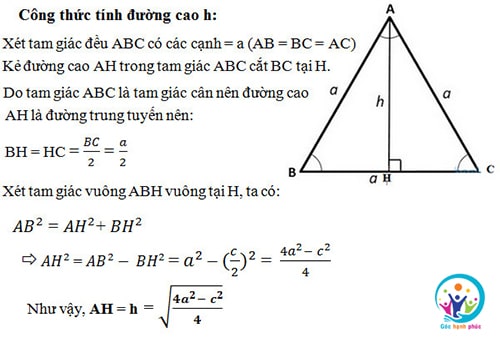
Công thức tính đường cao tam giác đều
Ví dụ minh họa: Giả sử trong tam giác ABC có độ dài cạnh bằng a

Công thức tính đường cao trong tam giác thường
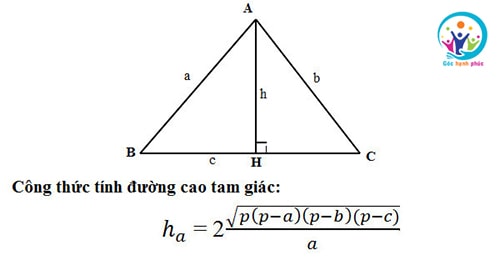
Trong đó: a, b, c lần lượt là độ dài các cạnh trong tam giác
h là chiều cao của tam giác
Bài tập có lời giải về cách tính đường cao trong tam giác
Bài tập trắc nghiệm
Bài tập 1: Cho ∆MNP, 2 đường cao MI và NJ cắt nhau tại H. Chọn đáp án đúng.
A. H là trọng tâm của ∆MNP
B. H là tâm đường tròn nội tiếp ∆MNP
C. PH là đường cao của ∆MNP
D. PH là đường trung trực của ∆MNP
Bài tập 2: Cho ∆MNP cân tại M biết MI là đường trung tuyến khi đó
A. MINP ﬩
B. MI là đường trung trực của NP
C. MI là đường phân giác của góc NMP
D. A, B, C đều đúng
Lời giải
Bài tập 1: C
Bài tập 2: D
Lời giải: vì ∆MNP cân tại M có MI là đường trung tuyến nên MI cũng là đường cao, đường trung trực và là đường phân giác của ∆MNP
Bài tập tự luận
Bài tập 1: Cho 2 đường thẳng xx’ và yy’ cắt nhau tạo I. Trên Ix, Ix’ lần lượt lấy các điểm B, D sao cho IA = IB, IC = ID. Gọi M, N lần lượt là trung điểm của cạnh AB và CD. Chứng minh M, I, N thẳng hàng
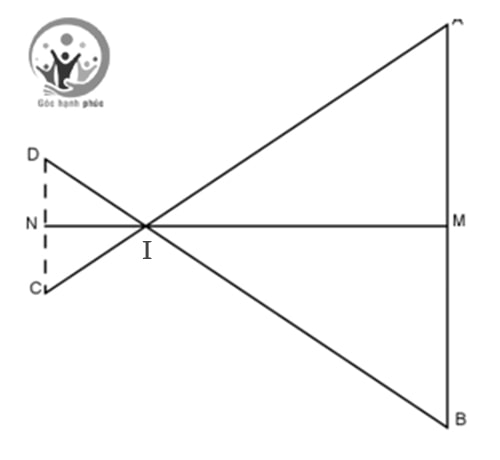
Lời giải
Ta có IA = IB (gt)
Nên ∆IAB cân tại I
IC = ID (gt)
=> ∆ICD cân tại I
Trong ∆IAB cân tại I có AM là đường trung tuyến và IM là đường phân giác của góc I
Tương tự ta có IN là đường phân giác của góc I
Im, IN là 2 tia phân giác của 2 góc đối đỉnh
Vậy I, M , N thẳng hàng
Bài tập 2: Cho ∆ABC vuông tại A có đường cao AH, biết AB : AC = 3, AB + AC = 21cm
- Tính độ dài các cạnh của ∆ABC
- Tính đường cao AH

Hy vọng với những thông tin trên của chúng tôi về công thức tính đường cao trong tam giác cân, vuông, đều, thường và những bài tập có lời giải sẽ giúp các em học sinh nhớ công thức lâu hơn và áp dụng công thức để giải bài toán từ cơ bản đến nâng cao thành công, đem lại thành tích học tập xuất sắc nhất. Nếu như các em còn thắc mắc gì hoặc có bài tập nào đang khó khăn hãy để lại comment bên dưới chúng tôi sẽ giải đáp thắc mắc nhanh nhất.







