Công thức tính góc giữa hai đường thẳng chi tiết và bài tập

Trong toán học được phân ra làm 2 dạng và toán hình và toán số. Thông thường các bạn học sinh sẽ cảm thấy khó hơn khi học toán hình. Đặc biệt vấn đề đang được nhiều bạn học sinh tìm kiếm chính là “công thức tính góc giữa hai đường thẳng trong không gian”. Đây cũng là một trong những kiến thức quan trọng mà còn nhiều em bỏ quên. Bài viết hôm nay chúng tôi sẽ giúp bạn hiểu về khái niệm, công thức và cho bài tập góc giữa hai đường thẳng, mời bạn đọc cùng đón xem nhé.

Xem thêm:

• Công thức tính khoảng cách giữa hai đường thẳng và ví dụ minh họa
• Công thức tính khoảng cách từ điểm đến đường thẳng và bài tập minh họa

Khái niệm về góc giữa hai đường thẳng

Trong không gian cho hai đường thẳng a và b bất kỳ. Từ một điểm O nào đó ta vẽ 2 đường thẳng lần lượt là a’ và b’ song song với a và b. Ta nhận thấy rằng khi điểm O thay đổi thì góc giữa hai đường thẳng a và b không hề thay đổi.

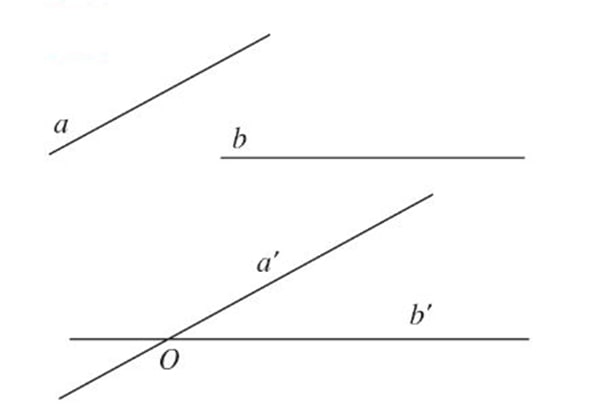
Góc giữa hai đường thẳng trong không gian được hiểu là góc giữa hai đường thẳng cùng đi qua một điểm và nó lần lượt song song với hai đường thẳng đã cho ban đầu.

Cách xác định góc giữa hai đường thẳng trong không gian

Để xác định được góc giữa hai đường thẳng trong không gian a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ thêm một đường thẳng đi qua O và nó song song với đường thẳng còn lại như sau.

Hay ta có thể sử dụng tích vô hướng như sau:

• Nếu vecto u là vecto chỉ phương của đường thẳng a và vecto v là vecto chỉ phương của đường thẳng b và (vecto u; vecto v) = α thì góc giữa hai đường thẳng a và b = α nếu 0 ≤ α ≤ 90⁰ và = 180⁰ – α nếu 90⁰ < α ≤ 180⁰.
• Nếu hai đường thẳng a và b song song hay trùng với nhau thì góc giữa nó sẽ bằng 0⁰. Góc giữa hai đường thẳng chính là góc có số đo 0 ≤ α ≤ 90⁰.

Công thức tính góc giữa hai đường thẳng trong không gian chính xác

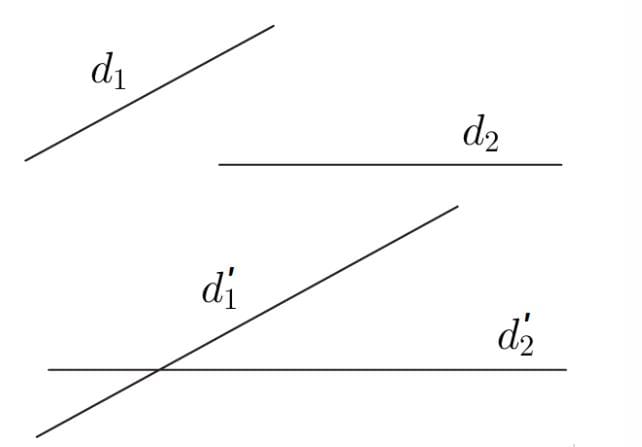
Trong không gian cho hệ trục tọa độ Oxyz, cho hai đường thẳng d₁, d₂. Gọi vecto u₁ = (a₁; b₁; c₁) và vecto u₂ = (a₂; b₂; c₂). Lần lượt là vecto chỉ phương của d₁ và d₂. Khi đó cosin của góc giữa hai đường thẳng này được tính theo công thức như sau:

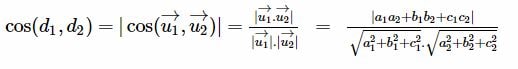
Công thức tính góc giữa hai đường thẳng trong mặt phẳng đầy đủ

1. Cách tính theo góc giữa hai vecto chỉ phương

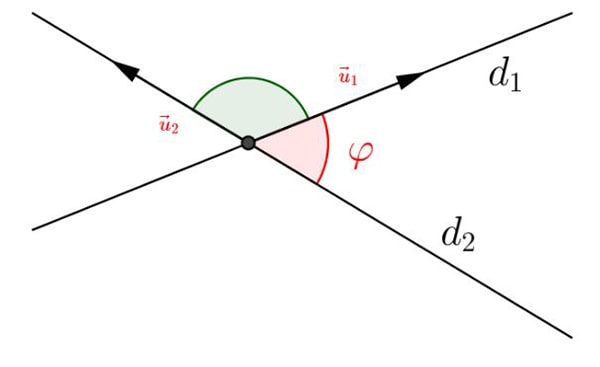
Trong mặt phẳng hệ trục tọa độ Oxy, cho hai đường thẳng d₁ và d₂. Gọi vecto u₁ = (a₁; b₁) và vecto u₂ = (a₂; b₂) lần lượt là vecto chỉ phương của d₁ và d₂. Khi đó, cos của góc giữa hai đường thẳng sẽ được tính theo công thức như sau:

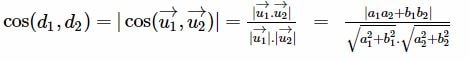
2. Cách tính theo góc giữa hai vecto pháp tuyến

Gọi vecto n₁ = (A₁; B₁) và vecto n₂ = (A₂; B₂) lần lượt là vecto pháp tuyến của d₁ và d₂. Khi đó, góc giữa hai đường thẳng này sẽ được tính theo công thức như sau:

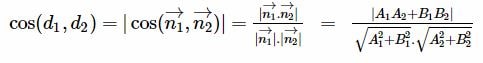
Bài tập tính góc giữa hai đường thẳng có lời giải dễ hiểu

Bài tập 1: Hãy tính góc giữa hai đường thẳng (a): 3x + y – 3 = 0 và (b): 2x – y + 29 = 0?

Lời giải

Đường thẳng 3x + y – 3 = 0 có VTPT vecto n (3; 1)

Đường thẳng 2x – y + 29 = 0 có VTPT vecto n (2; -1)

Cos(a; b) = |cos(vecto n_a; vecto n_b)|

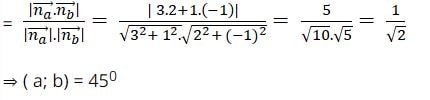
Bài tập 2: Tìm cosin góc giữa hai đường thẳng Δ₁: 10x + 5y – 2 = 0 và Δ₂:

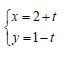
Lời giải

Vecto pháp tuyến của Δ₁ và Δ₂ lần lượt là vecto n₁ = (2;1) và vecto n₂ = (1;1)

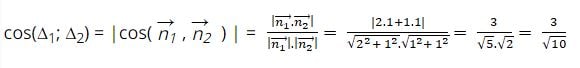
Hy vọng rằng với những kiến thức về góc giữa hai đường thẳng mà chúng tôi vừa chia sẻ ở trên sẽ giúp bạn đọc nhớ công thức và dễ dàng giải những bài tập toán liên quan nhé.