Khai triển nhị thức newton là kiến thức môn Toán Học lớp 11. Đây là một trong những kiến thức quan trọng thường được áp dụng vào kỳ thi cuối kỳ, thi THPT. Mà việc khai triển nhị thức newton chưa bao giờ là dễ dàng nếu như bạn không thực sự tập trung, thuộc công thức khai triển nhị thức newton và thường xuyên làm bài tập.
Do vậy, để giúp các em học sinh nắm vững về nhị thức newton, nhớ công thức và có thể giải nhiều dạng bài toán khai triển nhị thức newton thì Top Nổi Bật đã tổng hợp kiến thức, công thức và bài tập nhị thức newton lớp 11. Mời bạn đọc xem bài viết dưới đây nhé.
Định nghĩa khai triển nhị thức newton
Trong toán học lớp 11, định nghĩa khai triển nhị thức newton là một định nghĩa về việc khai triển hàm mũ của tổng. Kết quả tìm được của việc khai triển nhị thức newton là việc khai triển một nhị thức bậc n thành một đa thức có n + 1 số hạng như sau:
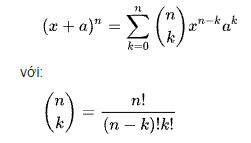
Công thức khai triển nhị thức newton lớp 11
Với n là số nguyên dương, hai số a, b là các số thực thì ta được công thức khai triển nhị thức newton như sau:
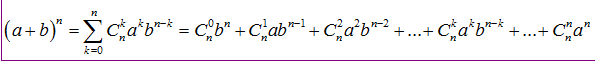
Bởi vai trò của a và b giống nhau nên hoán đổi vị trí a và b ta có một công thức tương đương như sau:
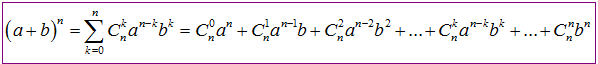
Lưu ý: Để giúp các em học sinh dễ nhớ về công thức này thì hãy để ý trong mỗi số hạng tổng số mũ của a và b luôn bằng n, và trong mỗi khai triển sẽ có n + 1 số hạng.
Áp dụng công thức khai triển nhị thức ở trên ta có thể khai triển một số hằng đẳng thức quen thuộc như sau:
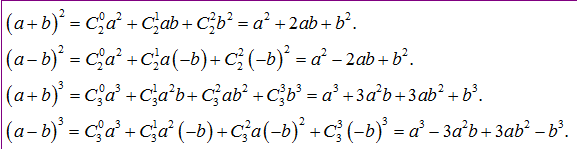
Một số bài tập khai triển nhị thức newton có lời giải chi tiết
Bài tập 1: Tính tổng
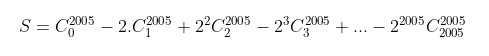
Lời giải
Áp dụng công thức trên với a = 1, b = -2 ta được:
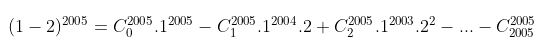
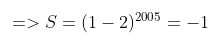
Đáp số: S = -1
Bài tập 2: Tìm hệ số của x3 trong khai triển nhị thức newton của (x2 + 3/x)12
Lời giải
Áp dụng công thức khai triển newton ta có:
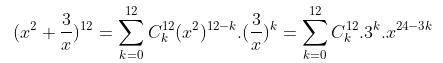
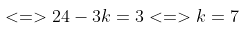
Vậy hệ số của x3 trong khai triển của
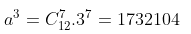
Trên đây là toàn bộ kiến thức về khai triển nhị thức Newton mà chúng tôi tổng hợp. Do vậy, các em học sinh chỉ cần học thuộc công thức và chịu khó làm nhiều bài tập từ cơ bản đến nâng cao. Nếu chỉ học thuộc công thức thì các em sẽ rất dễ quên. Do vậy, đừng quên làm nhiều bài tập, áp dụng đúng theo công thức nhé.
Có thể bạn quan tâm:
- Các công thức hạ bậc lượng giác và bài tập có lời giải
- Tổng hợp công thức tổ hợp, chỉnh hợp, hoán vị, xác xuất, và nhị thức Newton








